Math for devs - Relational Algebra
February 25, 2023
Do you remember set theory? A math topic that you probably learned in elementary school, revisited in high school, and then never again? Well, it's time to revisit it. Relational Algebra is a formal language based on set theory, and it's purpose is to query and manipulate data. But attention! Relational Algebra is not a programming language, it's more like a math notation, a formal and theoretical language.
Why do I need to know this?
Relational Algebra is the basis for SQL, the main language used in relational databases. Relational Algebra can also have some applications in NoSQL databases. If you want to understand how databases work "under the hood", you need to know the main concepts of Relational Algebra.
What is Relational Algebra?
Relational algebra is a declarative language for querying and manipulating data. As SQL, you just specify which data you want, what conditions it should satisfy, and how it should be transformed (grouped, sorted, aggregated, etc). The database engine will take care of the rest, so you don't have to worry about how the data is stored, nor how to access it.

In the image above, we have a woman who wants to order a pizza. She doesn't know how to make a pizza, she doesn't know how to cook it, she doesn't know how to deliver it. She just knows what she wants, and she knows how to ask for it. The waiter is the SQL/Relational Algebra engine, he is an interface between the woman and the chef. The chef is the database engine, he understands the order passed by the waiter, and he knows how to make the pizza.
Declarative query languages usually hide the implementation details from the user. This is a good thing, because it allows the database engine to optimize the query execution, and it also allows the user to focus on the data, not on the algorithm required to access it.
SQL analogy
How to order a pizza in SQL:
SELECT * FROM pizza
WHERE size = 'large'
AND flavor = 'pepperoni';
How to order a pizza in Relational Algebra:
Relational Algebra Operations
Ted Codd, a mathematician and computer scientist, proposed eight operations for Relational Algebra. These operations are:
- Selection ()
- Projection ()
- Cartesian Product ()
- Union ()
- Difference ()
- Join ()
- Division ()
- Intersection ()
In this article, we will only cover the first six operations. The other four are more advanced, and they are not widely used in practice.
Before we dive into the details of each operation, let's define our dataset. We will use a simple dataset with two tables:
Table 1: Players
| id | name | phone | countryId | |
|---|---|---|---|---|
| 1 | Lionel Messi | leomessi@afa.com | +54 9111234-5678 | 1 |
| 2 | Cristiano Ronaldo | cr7@siii.pt | +351 912345-678 | 2 |
| 3 | Pele | pele@goat.br | +55 91234-5678 | 3 |
| 4 | Diego Maradona | maradona@afa.com | +54 911234-5678 | 1 |
Table 2: Countries
| id | name | code |
|---|---|---|
| 1 | Argentina | AR |
| 2 | Portugal | PT |
| 3 | Brazil | BR |
Selection ()
The selection operation is used to filter the rows of a table. It is represented by the symbol .
The condition is a boolean expression that must be satisfied by the rows of the table. The result of the selection is a new (SET) table with only the rows that satisfy the condition.
Example
Let's say we want to select all the players from Argentina. We can do that with the following query:
SELECT * FROM players
WHERE countryId = 1;
The equivalent query in Relational Algebra is:
The result of the selection is a new table with only the players from Argentina:
| id | name | phone | countryId | |
|---|---|---|---|---|
| 1 | Lionel Messi | leomessi@afa.com | +54 9111234-5678 | 1 |
| 4 | Diego Maradona | maradona@afa.com | +54 911234-5678 | 1 |
Projection ()
Instead of selecting rows, like the selection operation, the project operation selects columns. It is represented by the symbol . This operation allows us to filter the columns of a table.
The columns argument is a list of column names. The result of the projection is a new table with only the columns specified in the columns argument.
Example
Projection is very useful when we want to select only a few columns from a table. Let's say we want to select the name and email of all the players.
SELECT name, email FROM players;
The equivalent query in Relational Algebra is:
The result of the projection is a new table with only the name and email columns:
| name | |
|---|---|
| Lionel Messi | leomessi@afa.com |
| Cristiano Ronaldo | cr7@siii.pt |
| Pele | pele@goat.br |
| Diego Maradona | maradona@afa.com |
We can also combine the selection and projection operations. Let's say we want to select the name and email of all the players from Argentina.
SELECT name, email FROM players
WHERE countryId = 1;
The equivalent query in Relational Algebra is:
In the expression above, we first apply the projection operation, to specify which columns we want to be returned by the query. Then, we apply the selection operation, to filter the rows of the table, containing only argentinian players.
Union ()
The union operation is the equivalent of the SQL UNION operator. It is used to combine the rows of two tables. The result of the union operation is a new table with the rows of both tables.
To perform the union operation, the tables must have the same number of columns, and the columns must have the same data types.
Example
Let's say we want to combine the players from Argentina and Brazil. We can do that with the following query:
SELECT * FROM players
WHERE countryId = 1
UNION
SELECT * FROM players
WHERE countryId = 3;
The equivalent query in Relational Algebra is:
In the expression above, we first query the players from Argentina, then we store the result in the ARGENTINIAN_PLAYERS variable. The same process is repeated for the players from Brazil, and the result is stored in the BRAZILIAN_PLAYERS variable. Finally, we apply the union operation to combine the rows of both tables. The result of the union operation is a new table with the players from Argentina and Brazil:
| id | name | phone | countryId | |
|---|---|---|---|---|
| 1 | Lionel Messi | leomessi@afa.com | +54 9111234-5678 | 1 |
| 4 | Diego Maradona | maradona@afa.com | +54 911234-5678 | 1 |
| 3 | Pele | pele@goat.br | +55 91234-5678 | 3 |
Difference ()
With the difference operator, we have as result the rows of the first table that are not present in the second table. It is represented by the symbol .
Everything that exists in the subset and does not exist in the superset is the difference between and .
You probably already saw an image like this one:
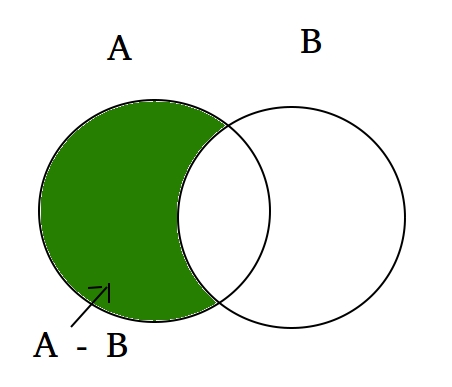
Example
Let's say we want to get all the players that are not brazilian. We can do that with the following query:
SELECT * FROM players
EXCEPT
SELECT * FROM players
WHERE countryId = 3;
The equivalent query in Relational Algebra is:
Cartesian Product ()
The cartesian product operation is the equivalent of the SQL CROSS JOIN operator. It is used to combine the rows and columns of two tables. For example, if you have a table "A" with 3 columns and a table "B" with 2 columns, the result of the cartesian product operation is a new table with 5 columns, containing every single combination of rows from table "A" and table "B".
Example
Let's say we want to get all the possible combinations of players and countries. We can do that with the following query:
SELECT * FROM players
CROSS JOIN countries;
The equivalent query in Relational Algebra is:
The result of the cartesian product operation is a new table with 5 columns, containing every single combination of rows from table "players" and table "countries":
| id | name | phone | countryId | id | name | code | |
|---|---|---|---|---|---|---|---|
| 1 | Lionel Messi | leomessi@afa.com | +54 9111234-5678 | 1 | 1 | Argentina | AR |
| 2 | Cristiano Ronaldo | cr7@siii.pt | +351 912345-678 | 2 | 2 | Portugal | PT |
| 3 | Pele | pele@goat.br | +55 91234-5678 | 3 | 3 | Brazil | BR |
| 4 | Diego Maradona | maradona@afa.com | +54 911234-5678 | 1 | 1 | Argentina | AR |
Join ()
The join operation is the equivalent of the SQL JOIN operator. It is used to combine the rows of two tables, based on a common column. The result of the join operation is a new table with the columns of both tables.
To perform the join operation, the tables must have at least one column in common. If there are no common columns, the result of the join operation is an empty table.
Example
Let's say we want to get the name and email of all the players, along with the name of the country they are from. We can do that with the following query:
SELECT players.name, players.email, countries.name, clubs.name
FROM players
JOIN countries ON players.countryId = countries.id;
The equivalent query in Relational Algebra is:
In the expression above, we first apply the projection operation, to specify which columns we want to be returned by the query. Then, we apply the join operation, to combine the rows of the players table and the countries table, based on the countryId column. Finally, we apply the rename operation, to rename the id column to countryId.
The result of the join operation is a new table with the name, email, and country name of all the players:
| name | countryName | |
|---|---|---|
| Lionel Messi | leomessi@afa.com | Argentina |
| Cristiano Ronaldo | cr7@siii.pt | Portugal |
| Pele | pele@goat.br | Brazil |
| Diego Maradona | maradona@afa.com | Argentina |
Conclusion
Now you already know the basics of Relational Algebra. If you want, you can do some extra research on the subject, and learn more about the other operations that are available in Relational Algebra.